GSEB Solutions Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise

Gujarat Board GSEB Textbook Solutions Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise Textbook Questions and Answers.

Gujarat Board Textbook Solutions Class 12 Maths Chapter 8 Application of Integrals Miscellaneous Exercise

Question 1.
Find the area under the following given curves and given lines:
(i) y = x², x = 1, x = 2 and x-axis.
(ii) y = x⁴, x = 1, x = 5 and x-axis.
Solution:
(i) Graphs of parabola y = x², lines x = 1, x = 2 and x-axis are shown in the figure.
The area of region bounded by y = x², x = 1, x = 2 and x-axis.
= Area of region PLMQP

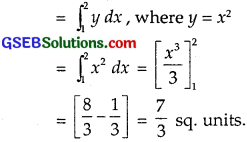
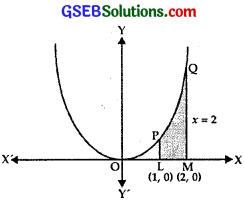
(ii) The curve y = x⁴ passes through (0, 0) and it is symmetric about y-axis for all x ∈ R.

∴ \(\frac{dy}{dx}\) = 4x³.
\(\frac{dy}{dx}\) = 0 at x = 0.
\(\frac{dy}{dx}\) changes sign from – ve to + ve as x increases through x = 0
∴ y is minimum at x = 0.
When x > 0, y is the increasing function.
Graph is as shown in the figure.
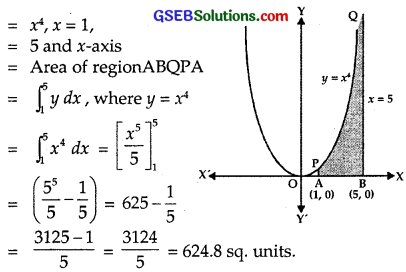
Area of region bounded by
y = x⁴, x = 1,
x = 5 and x-axis
= Area of region ABQPA

Question 2.
Find the area between the curves y = x and y = x².
Solution:
Given curves are
y = x …………… (1)
y = x² ……………… (2)
Putting y = x in eq.(2), we get
x = x²
∴ x = 0, 1
When x = 1, y = 1

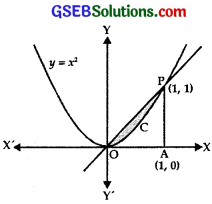
These curves intersect at (0, 0) and (1, 1).
∴ Area between y = x
and y = x²
= Area of the region OCPQ
= Area of OAP – Area of region OAPCO

Question 3.
Find the area of the region lying in first quadrant and bounded by y = 4x², x = 0, y = 1 and y = 4.
Solution:
The given curve and lines which bound the region are
y = 4x², x = 0, y = 1 and y = 4.
Graph is as shown in the figure.
The area of the region lying in the first quadrant and bounded by
y = 4x², x = 0, y = 1 and y = 4

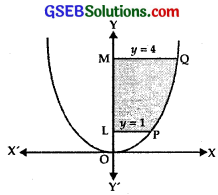
= Area of the region = LPQML
= Area OQMO – Area OPLO

Question 4.
Sketch the graph of y = |x + 3| and evaluate \(\int_{6}^{0}\) |x + 3| dx.
Solution:
y = |x + 3|
At x = – 3, y = 0
AQ is the line y = x + 3.
When x + 3 < 0,
y = -(x + 3)
= – x – 3

Graph of the line is AP.
∴ Graph of y = |x + 3| is as shown in the figure.

Question 5.
Find the area bounded by the curve y = sin x between x = 0 and x = 2π.
Solution:
Some points on the sine graph are:

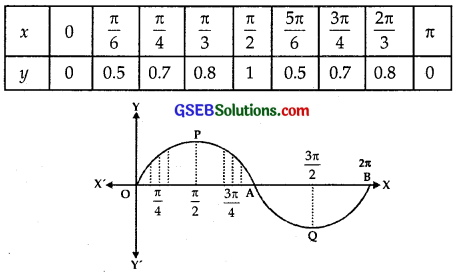
Plotting these points, we get the graph OPAQB.
Since sin(2π – x) = – sin x, therefore
graph between x = π and x = 2π has the same shape but it is below the x-axis.
Area of the region OPA = Area of the region AQB.
∴ Area bounded by the curve y = sin x between x = 0 and x = 2π.
= 2 × Area of the region OPA

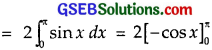
= – 2[cos π – cos 0] = 2[1 + 1] = 4.

Question 6.
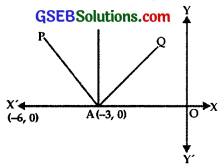
Find the area enclosed between the parabola y² = 4ax and the line y = mx.
Solution:
The given curves are
y = mx …………….. (1)
y² = 4ax …………….. (2)
Putting value of y from (1) in (2), we get
m²x² = 4ax
or x(m²x – 4a) = 0
∴ x = 0, x = \(\frac{4 a}{m^{2}}\).
Putting x = \(\frac{4 a}{m^{2}}\) in (1),
y = m.\(\frac{4 a}{m^{2}}\) = \(\frac{4a}{m}\)

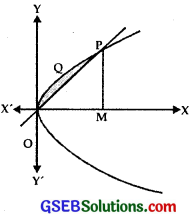
∴ The curve y² = 4ax and OP intersect at O(0, 0) and
∴ Area enclosed between the parabola y² = 4ax and the line y = mx.
= Area of the region OPOQ [As per figure]
= Area of the region OMPQO – Area of ∆ OMP

Question 7.
Find the area enclosed by the parabola 4y = 3x² and the line 2y = 3x + 12.
Solution:
The parabola and the line are
4y = 3x² …………………. (1)
2y = 3sx + 12 ………………. (2)
Multiplying (2) by 2 and
Subtracting from (1), we get
0 = 3x² – 6x – 24
or x² – 2x – 8 = 0
or (x – 4)(x + 2) = 0
∴ x = 4, – 2
From (2), y = 12, 3

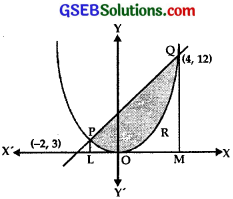
The graph of parabola and lines are shown in the figure. They intersect at P(- 2, 3) and Q(4, 12).
∴ The area enclosed by the parabola 4y = 3x²
and the line 2y = 3x + 12
= Area of the region POPQP
= Area of trapezium PLMQP – Area of the region LMQROP

= 45 – 18 = 27 sq.units.

Question 8.
Find the area of the smaller region bounded by the ellipse
\(\frac{x^{2}}{9}\) + \(\frac{y^{2}}{4}\) = 1 and the straight line \(\frac{x}{3}\) + \(\frac{y}{2}\) = 1.
Solution:

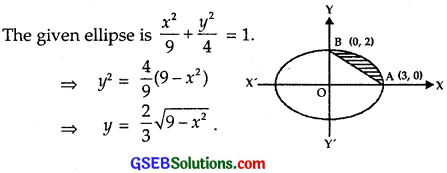
It is an ellipse with vertices at A(3, 0) and B(0, 2) and length of the major axis = 2(3) = 6 and length of the minor axis 2(2) = 4.
Line \(\frac{x}{3}\) + \(\frac{y}{2}\) = 1 ⇒ y = (\(\frac{6-2x}{3}\))
It is a straight line passing through A(3, 0) and B(0, 2).
Smaller area common to both is shaded.

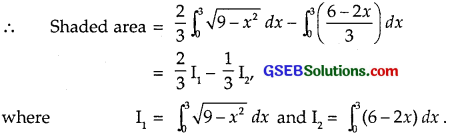
For I₁ put x = 3 sin θ so that dx = 3 cos θ dθ.
When x = 0, θ = 0 and when x = 3, θ = \(\frac{π}{2}\)

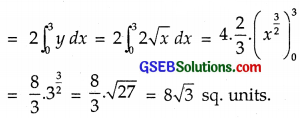
Question 9.
Find the area of the smaller region bounded by the ellipse
\(\frac{x^{2}}{a^{2}}\) + \(\frac{y^{2}}{b^{2}}\) = 1 and the staraight line \(\frac{x}{a}\) + \(\frac{y}{b}\) = 1.
Solution:

Question 10.
Find the area of the region enclosed by parabola x² = y, the line y = x + 2 and the x-axis.
Solution:
We have x² = y. It represents a parabola with vertex at (0, 0), axis along the positive direction of y-axis and it opens upwards.
Also, y = x + 2 represents a straight line cutting x-axis at (-2, 0).
Solving x² = y and y = x + 2, we get
x² = x + 2
⇒ x² – x – 2 = 0
⇒ (x – 2)(x + 1) = 0
⇒ x = 2, x = 1.
⇒ When x = 2, y = (2)² = 4
and when x = – 1, y = (- 1)² = 1.

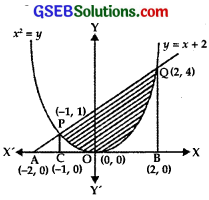
So the two curves x² = y and y = x + 2 intersect at the points (2, 4) and (- 1, 1).
Required area = Shaded region shown in the figure

Question 11.
Using method of integration, find the area bounded by |x| + |y| = 1.
Solution:
In I Quadrant, x > 0 and y > 0.
⇒ |x| = x, |y| = y.
The line is x + y = 1 …………….. (1)
In II Quadrant, x < 0 and y > 0.
⇒ |x| = – x. |y| = y.
The line is – x + y = 1
or x – y = -1 ………………… (2)
In III Quadrant, x < 0 and y < 0. ⇒ |x| = – x, |y| = – y. The line is – x – y = 1 or x + y = -1 ………….. (3)
In IV Quadrant, x > 0 and y < 0.
⇒ |x| = x, |y| = – y,
The line is x – y = 1 …………. (4)
Thus, |x| + |y| = 1 represent four lines forming a square ABCD.
Area of square ABCD

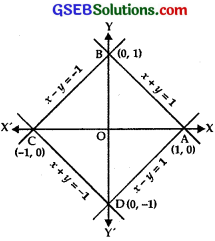
= 4 × Area of ∆ AOB
= 4 × \(\int_{0}^{1}\) (1 – x) dx
Since x + y = 1 is the equation of the line AB.

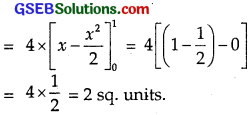
= 4 × \(\frac{1}{2}\) = 2 sq.units.

Question 12.
Find the area bounded by the curves {(x, y) y = ≥ x² and y = |x|}.
Solution:
Clearly, x² = y represents parabola with vertex at (0, 0), positive direction of y-axis as its axis and it opens upwards.
y= | x |, i.e., y = x and y = – x represent two lines passing through the origin and making an angle of 45° and 135° with the positive direction of the x-axis.

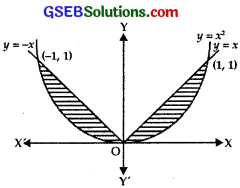
The required region is the shaded region as shown in the figure. Since both the curves are symmetrical about y-axis, therefore
required area = 2(shaded area in the first quadrant)

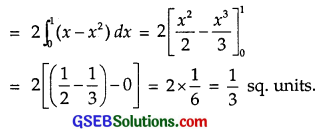
Question 13.
Using the method of integration, find the area of the triangle ABC, coordinates of whose vertices are A(2, 0), B(4, 5) and C(6, 3).
Solution:
Equation of the line AB is
y – 0 = \(\frac{5-0}{4-2}\)(x – 2)
⇒ y = \(\frac{5}{2}\)(x – 2).
Equation of the line BC is
y – 5 = \(\frac{3-5}{6-4}\)(x – 4)
⇒ y = – x + 9.
Equation of the line CA is
y – 3 = \(\frac{0-3}{2-6}\)(x – 6)
⇒ y = \(\frac{3}{4}\)(x – 2).

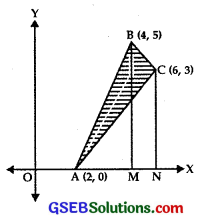
Required area = area of the region bounded by ∆ ABC
= area of the region AMB + area of the region BMNC – area of the region ANC

= 5 + 8 – 6 = 7 sq. units.

Question 14.
Using the method of integration, find the area of the region bounded by the lines
2x + y = 4, 3x – 2y = 6 and x – 3y + 5 = 0.
Solution:
The given lines are 2x + y = 4 ………….. (1)
3x – 2y = 6 ……………….. (2)
x – 3y = – 5 ……………….. (3)
Multiplying (3) by 2 and subtracting from (1), we get
7y = 14 ⇒ y = 2.
So, from (3) x – 6 = 5 ⇒ x = 1.
∴ Lines (1) and (3) intersect at (1, 2).
Again multiplying (3) by 3 and subtract it from (2). We get
7y = 21 ∴ y – 3.
From (3), X – 9 = – 5 ⇒ x = 4.
∴ Lines (2) and (3) intersect at (4, 3).
Multiply eq. (1) by 2 and add it to (2).
We get: 7x = 14 ∴ x = 2
From (2), 4 + y – 4 ∴ y = 0.
Lines (1) and (2) intersect at (2, 0).
The points A(1, 2), B(4, 3) and C(2, 3) are plotted and joined obtaining triangle ABC.

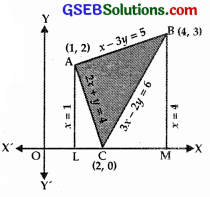
Area of ∆ ABC = Area of trapezium ALMB – Area of ∆ ALC – Area of ∆ BCM

Question 15.
Find the area of the region {(x, y) : y² ≤ 4x, 4x² + 4y² ≤ 9}.
Solution:
y² = 4x is a parabola whose vertex is the origin and 4x² + 4y² = 9
represents a circle whose centre is (0, 0) and radius = \(\frac{3}{2}\).
On solving y² = 4x
and x² + y² = \(\frac{9}{4}\).
The points of intersection are P(\(\frac{1}{2}\), \(\sqrt{2}\)) and Q(\(\frac{1}{2}\), – \(\sqrt{2}\)).
Both the curves are symmetrical about x-axis

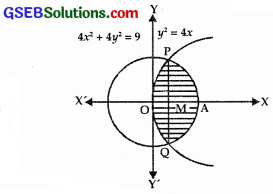
Required area = area of the shaded region
= 2(area of the region OAPO)
= 2[(area of the region OMPO) + (area of the region MAPM)]

Choose the correct answers in the following questions 16 to 19:

Question 16.
The area bounded by the curve y = x³, the x-axis and ordinates x = – 2 and x = 1 is
(A) – 9
(B) – \(\frac{15}{4}\)
(C) \(\frac{15}{4}\)
(D) \(\frac{17}{4}\)
Solution:
The curve is y = x³.
Differentiating, we get
\(\frac{dy}{dx}\) = 3x² = +ve

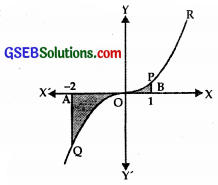
∴ Curve is an increasing curve.
\(\frac{dy}{dx}\) = 0 ⇒ x = 0.
∴ x-axis is the tangent at x = 0.
f(- x) = – f(x) ∴ (- x)³ = – x³.
Curve is symmetrical in opposite quadrants,
Area bounded by the curve y = x³, the x-axis, x = – 2 and x = 1
= Area of the region AQOBPOA
= Area of the region AQOA + Area of the region ∆ BPO

∴ Part D is the correct answer.

Question 17.
The area bounded by the curve y = x |x|, x-axis and the ordinates x = – 1 and x = 1 given by
(A) 0
(B) \(\frac{1}{3}\)
(C) \(\frac{2}{3}\)
(D) \(\frac{4}{3}\)
Solution:
When x > 0, |x| = x.
∴ The equation of the curve is y = x².
When x < 0, |x| = – x.
∴ Equation of the curve is
y = x².
∴ Area bounded by the curve
y = x|x|,
x-axis and ordinates x = – 1, x = 1
= Area of region + Area of region ∆ BQO

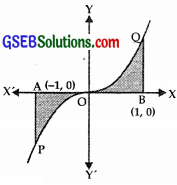
= 2 × Area of region ∆ BQO
(∵ These areas are equal due to symmetry)

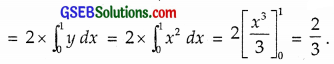
∴ Part (C) is the correct answer.

Question 18.
The area of the circle x² + y² = 16 exterior to the parabola y² = 6x is
(A) \(\frac{4}{3}\) (4π – \(\sqrt{3}\))
(B) \(\frac{4}{3}\) (4π + \(\sqrt{3}\))
(C) \(\frac{4}{3}\) (8π – \(\sqrt{3}\))
(D) \(\frac{4}{3}\) (8π + \(\sqrt{3}\))
Solution:
The given curves are
x² + y² = 16 ………….. (1)
y² = 6x ……………….. (2)
Putting y² = 6x in (1), we get
x² + 6x = 16
or x² + 6x – 16 = 0
(x + 8)(x – 2) = 0
∴ x = – 8, 2
But x ≠ – 8
So, x = 2.
From (2), y² = 6x ⇒ y = ± 2\(\sqrt{3}\)

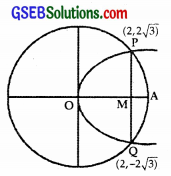
Area of the whole circle

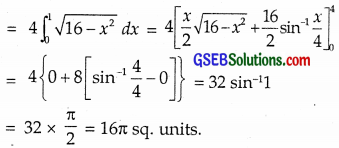
Now circle and parabola intersect at P(2, 2\(\sqrt{3}\)) and Q (2, – 2\(\sqrt{3}\)).
Smaller area enclosed by circle and parabola
= Area of region OQAP
= 2 × Area of region OQAP
= 2 × [Area of region OMP + Area of region MAP]
= 2(\(\int_{0}^{2} y_{1} d x+\int_{2}^{4} y_{2} d x\))
When y₁ is for parabola y² = 6x. ∴ y = \(\sqrt{6x}\).
y₂ is for circle x² + y² = 16 ∴ y = \(\sqrt{16-x^{2}}\)

Common area exterior to the parabola y² = 6x is equal to
16π – (\(\frac{4 \sqrt{3}}{3}\) + \(\frac{16}{3}\)π)
= \(\frac{32}{3}\)π – \(\frac{4 \sqrt{3}}{3}\) = \(\frac{4}{3}\)(8π – \(\sqrt{3}\)).
∴ Part (C) is the correct answer.

Question 19.
The area bounded by y-axis, y = cos x and y = sin x, 0 ≤ x ≤ \(\frac{π}{2}\) is
(A) 2(\(\sqrt{2}\) – 1)
(B) \(\sqrt{2}\) – 1
(C) \(\sqrt{2}\) + 1
(D) \(\sqrt{2}\)
Solution:
The curve are y = cos x, y = sin x, 0 ≤ x ≤ \(\frac{π}{2}\).
The curve meet
where sin x = cos x.
or tan x = 1
⇒ x = \(\frac{π}{4}\).
sin \(\frac{π}{4}\) = cos \(\frac{π}{4}\) = \(\frac{1}{\sqrt{2}}\).

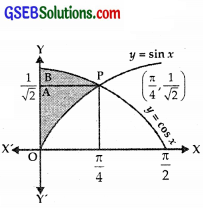
Graphs of these curves are as shown in the figure.
They intersect at P(\(\frac{π}{4}\), \(\frac{1}{\sqrt{2}}\)).
The area bounded by y-axis, y = cos x and y = sin x (0 ≤ x ≤ \(\frac{π}{2}\))
= shaded area
= Area of region ∆ OPBO
= Area of region ∆ PAO + Area of region ∆ PBA

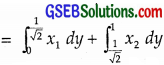
where x₁ is for y = sin x or x = sin^-1y ,
and x₂ is for y = cos x or x = cos^-1 y.

∴ Part (B) is the correct answer.