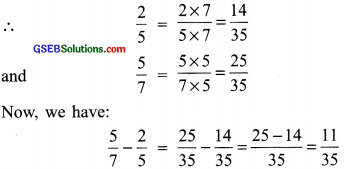Gujarat Board GSEB Textbook Solutions Class 6 Maths Chapter 7 Fractions InText Questions and Answers.
Gujarat Board Textbook Solutions Class 6 Maths Chapter 7 Fractions InText Questions
Try These (Page 137)
Question 1.
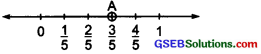
Show \(\frac { 3 }{ 5 }\) on a number line.
Solution:
We divide the length between 0 and 1 on a number line into 5 equal parts. The point A represents \(\frac { 3 }{ 8 }\)
![]()
Question 2.
Show \(\frac { 1 }{ 10 }\) , \(\frac { 0 }{ 10 }\) , \(\frac { 5 }{ 10 }\) and \(\frac { 10 }{ 10 }\) on a number line.
Solution:
We draw a number line. Divide the length between 0 and 1 into 10 equal parts.
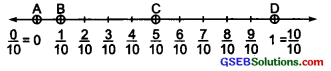
The point B represents \(\frac { 1 }{ 10 }\)
The point A represents \(\frac { 0 }{ 10 }\)
The point C represents \(\frac { 5 }{ 10 }\)
The point D represents \(\frac { 10 }{ 10 }\)
![]()
Question 3.
Can you show any other fraction between 0 and 1? Write five more fractions that you can show and depict them on the number line.
Solution:
Yes, we can show any number of fractions that are greater than 0 and less than 1.
Five other fractions, i.e. \(\frac { 2 }{ 3 }\) , \(\frac { 6 }{ 7 }\) , \(\frac { 1 }{ 8 }\) , \(\frac { 4 }{ 9 }\) and \(\frac { 4 }{ 5 }\) can be shown on a number line between 0 and 1. Direct these numbers on the number line by yourself.
![]()
Question 4.
How many fractions lie between 0 and 1? Think, discuss and write your answer.
Solution:
An infinite number of fractions lie between 0 and 1.
Try These (Page 138)
Question 1.
Give a proper fraction:
(a) Whose numerator is 5 and denominator is 7.
(b) Whose denominator is 9 and numerator is 5.
(c) Whose numerator and denominator add up to 10. How many fractions of this kind can you make?
(d) Whose denominator is 4 more than the numerator.
(Give any five. How many more can you make?)
Solution:
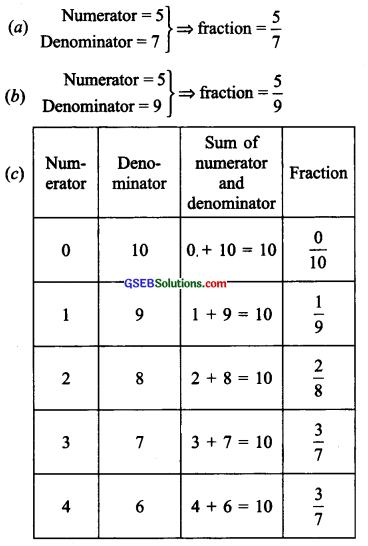
∴ Fractions whose numerator and denominator add up to 10 are: \(\frac { 0 }{ 10 }\) , \(\frac { 1 }{ 9 }\) , \(\frac { 2 }{ 8 }\) , \(\frac { 3 }{ 7 }\) and \(\frac { 4 }{ 6 }\).
(d) There can be infinite number of fractions whose denominator is 4 more than the numerator. Some of them are: \(\frac { 1 }{ 5 }\) , \(\frac { 2 }{ 6 }\) , \(\frac { 3 }{ 7 }\) , \(\frac { 4 }{ 8 }\) , \(\frac { 5 }{ 9 }\), etc.
![]()
Question 2.
A fraction is given. How will you decide, by just looking at it, whether, the fraction is (a) less than 1? (b) equal to 1?
Solution:

Question 3.
Fill up using one of these: ‘>’ , ‘<‘ or ‘=’
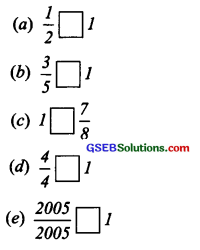
Solution:
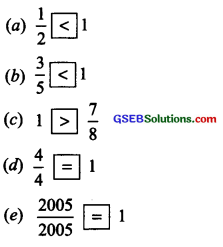
Try These (Page 142)
Question 1.
Are \(\frac { 1 }{ 3 }\) and \(\frac { 2 }{ 7 }\);\(\frac { 2 }{ 5 }\) and \(\frac { 2 }{ 7 }\);\(\frac { 2 }{ 9 }\) and \(\frac { 6 }{ 27 }\) equivalent? Give reason.
Solution:
(i) \(\frac { 1 }{ 3 }\) and \(\frac { 2 }{ 7 }\) ∵ 1 × 7 = 7, 3 × 2 = 6
and 7 ≠ 6, i.e. 1 × 7 ≠ 3 × 2
∴ \(\frac { 1 }{ 3 }\) and \(\frac { 2 }{ 7 }\) are not equivalent fractions.
(ii) \(\frac { 2 }{ 5 }\) and \(\frac { 2 }{ 7 }\) ∵ 2 × 7 = 14, 5 × 2 = 10
and 14 ≠ 10, i.e. 2 × 7 ≠ 5 × 2
∴ \(\frac { 2 }{ 5 }\) and \(\frac { 2 }{ 7 }\) are not equivalent fractions.
(iii) \(\frac { 2 }{ 9 }\) and \(\frac { 6 }{ 27 }\) ∵ 2 × 27 = 54, 9 × 6 = 54
and 54 = 54, i.e. 2 × 27 = 9 × 6
∴ \(\frac { 2 }{ 9 }\) and \(\frac { 6 }{ 27 }\) are equivalent fractions.
![]()
Question 2.
Give an example of four equivalent fractions.
Solution:
The following pairs of fractions are equivalent:
(i) \(\frac { 2 }{ 8 }\) and \(\frac { 1 }{ 4 }\)
(ii) \(\frac { 5 }{ 12 }\) and \(\frac { 15 }{ 36 }\)
(iii) \(\frac { 8 }{ 11 }\) and \(\frac { 16 }{ 22 }\)
(iv) \(\frac { 4 }{ 26 }\) and \(\frac { 2 }{ 13 }\)
Question 3.
Identify the fractions in each. Are these fractions equivalent?
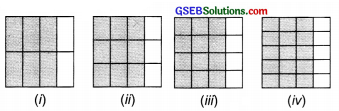
Solution:
(i) The given figure represents the fraction \(\frac { 6 }{ 8 }\)
We have: \(\frac { 6 }{ 8 }\) = \(\frac{6 \div 2}{8 \div 2}\) = \(\frac { 3 }{ 4 }\)
(ii) The given figure represents the fraction \(\frac { 9 }{ 12 }\)
We have: \(\frac { 9 }{ 12 }\) = \(\frac{9 \div 3}{12 \div 3}\) = \(\frac { 3 }{ 4 }\)
(iii) The given figure represents the fraction \(\frac { 12 }{ 16 }\)
We have: \(\frac { 12 }{ 16 }\) = \(\frac{12 \div 4}{16 \div 4}\) = \(\frac { 3 }{ 4 }\)
(iv) The given figure represents the fraction \(\frac { 15 }{ 20 }\)
We have: \(\frac { 12 }{ 16 }\) = \(\frac{12 \div 4}{16 \div 4}\) = \(\frac { 3 }{ 4 }\)
Since, all the fractions represent \(\frac { 3 }{ 4 }\),
i.e., \(\frac { 6 }{ 8 }\) = \(\frac { 9 }{ 12 }\) = \(\frac { 12 }{ 16 }\) = \(\frac { 15 }{ 20 }\) = ![]()
Thus, the given figures represent equivalent fractions.
Try These (Page 143)
Question 1.
Find five equivalent fractions of each of the following:
(i) \(\frac { 2 }{ 3 }\)
(ii) \(\frac { 1 }{ 5 }\)
(iii) \(\frac { 3 }{ 5 }\)
(iv) \(\frac { 5 }{ 9 }\)
Solution:

Try These (Page 146)
Question 1.
Write the simplest form of:
(i) \(\frac { 15 }{ 75 }\)
(ii) \(\frac { 16 }{ 72 }\)
(iii) \(\frac { 17 }{ 51 }\)
(iv) \(\frac { 42 }{ 28 }\)
(v) \(\frac { 80 }{ 24 }\)
Solution:
(i) \(\frac { 15 }{ 75 }\)
Factors of 15 are: 1, 3, 5 and 15
Factors of 75 are: 1, 3, 5, 15, 25 and 75
Common factors are: 1, 3, 5 and 15
∴ HCF of 15 and 75 = 15
Now, \(\frac { 15 }{ 75 }\) = \(\frac{15 \div 15}{75 \div 15}\) = \(\frac { 1 }{ 5 }\)
Thus, simplest form of \(\frac { 15 }{ 75 }\) is \(\frac { 1 }{ 5 }\)
(ii) \(\frac { 16 }{ 72 }\)
Factors of 16 are: 1, 2, 4, 6, 8 and 16
Factors of 72 are: 1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 36 and 72
∴ Common factors are: 1, 2, 4, 6 and 8
∴ HCF of 16 and 72 is 8.
Now \(\frac { 16 }{ 72 }\) = \(\frac{16 \div 8}{72 \div 8}\) = \(\frac { 2 }{ 9 }\)
Thus, the simplest form of \(\frac { 16 }{ 72 }\) is \(\frac { 2 }{ 9 }\)
(iii) \(\frac { 17 }{ 51 }\)
Factors of 17 are: 1 and 17
Factors of 51 are: 1, 3 and 17
The common factor is 17
∴ HCF of 17 and 51 = 17
Now \(\frac { 17 }{ 51 }\) = \(\frac{17 \div 17}{51 \div 17}\) = \(\frac { 1 }{ 3 }\)
Thus, the simplest form of \(\frac { 17 }{ 51 }\) is \(\frac { 1 }{ 3 }\)
(iv) \(\frac { 42 }{ 28 }\)
Factors of 42 are: 1, 2, 3, 6, 7, 14, 21 and 42
Factors of 28 are: 1, 2, 4, 7, 14 and 28
Common factors are: 1, 2, 7 and 14
∴ HCF of 42 and 28 = 14
Now \(\frac { 42 }{ 28 }\) = \(\frac{42 \div 14}{28 \div 14}\) = \(\frac { 3 }{ 2 }\)
Thus, the simplest form of \(\frac { 42 }{ 28 }\) is \(\frac { 3 }{ 2 }\)
(v) \(\frac { 80 }{ 24 }\)
Factors of 80 are: 1, 2, 4, 5, 8, 10, 16, 20, 40 and 80
Factors of 24 are: 1, 2, 3, 4, 6, 8, 12 and 24
Common factors are: 1, 2, 4 and 8
∴ HCF of 80 and 24 = 8
Now, \(\frac { 80 }{ 24 }\) = \(\frac{80 \div 8}{24 \div 8}\) = \(\frac { 10 }{ 3 }\)
Thus, the simplest form \(\frac { 80 }{ 24 }\) is \(\frac { 10 }{ 3 }\)
![]()
Question 2.
Is \(\frac { 49 }{ 64 }\) in its simplest form?
Solution:
∵ Factors of 49 are: 1,7 and 49
Factors of 64 are: 1, 2, 4, 8, 16, 32 and 64
The common factor is 1, i.e. 49 and 64 have no common factor other than 1.
∴ 49 and 64 are coprime, i.e. \(\frac { 49 }{ 64 }\) is in its simplest form.
Try These (Page 148)
Question 1.
You get one-fifth of a bottle of juice and your sister gets one-third of a bottle of juice. Who gets more?
Solution:
Let us divide a rectangle into 5 equal parts and shade one of them, i.e. one-fifth is shaded.

Now, divide the same rectangle into 3 equal parts and shade one of them, Le. one-third is shaded, obviously, one third is greater. Thus, your sister gets more juice.
Try These (Page 149)
Question 1.
(a) Which is the larger fraction?
(i) \(\frac { 7 }{ 10 }\) or \(\frac { 8 }{ 10 }\)
(ii) \(\frac { 11 }{ 24 }\) or \(\frac { 13 }{ 24 }\)
(iii) \(\frac { 17 }{ 102 }\) or \(\frac { 12 }{ 102 }\)
(b) Why are these comparisons easy to make?
Solution:
(a) (i) \(\frac { 7 }{ 10 }\) < \(\frac { 8 }{ 10 }\)
Denominators are same and 7 < 8
∴ \(\frac { 7 }{ 10 }\) < \(\frac { 8 }{ 10 }\)
(ii) \(\frac { 11 }{ 24 }\) and \(\frac { 13 }{ 24 }\)
Denominators are same and 11 < 13
∴ \(\frac { 11 }{ 24 }\) < \(\frac { 13 }{ 24 }\)
(iii) \(\frac { 17 }{ 102 }\) and \(\frac { 12 }{ 102 }\)
Denominators are same and 17 > 12
∴ \(\frac { 17 }{ 102 }\) and \(\frac { 12 }{ 102 }\)
(b) These comparisons are easy because these are like fractions.
![]()
Question 2.
(a) \(\frac { 1 }{ 8 }\) , \(\frac { 5 }{ 8 }\) , \(\frac { 3 }{ 8 }\)
(b) \(\frac { 1 }{ 5 }\) , \(\frac { 11 }{ 5 }\) , \(\frac { 4 }{ 5 }\) , \(\frac { 3 }{ 5 }\) , \(\frac { 7 }{ 5 }\)
(c) \(\frac { 1 }{ 7 }\) , \(\frac { 3 }{ 7 }\) , \(\frac { 13 }{ 7 }\) , \(\frac { 11 }{ 7 }\) , \(\frac { 7 }{ 7 }\)
Solution:
We can write the like fractions in ascending or in descending order according to the order of their numerators.
(a) \(\frac { 1 }{ 8 }\) , \(\frac { 5 }{ 8 }\) , \(\frac { 3 }{ 8 }\)
∵ 1 , 3 and 5 are in ascending order.
∴ \(\frac { 1 }{ 8 }\) , \(\frac { 3 }{ 8 }\) and \(\frac { 5 }{ 8 }\) are in ascending order and \(\frac { 5 }{ 8 }\) , \(\frac { 3 }{ 8 }\) and \(\frac { 1 }{ 8 }\) are in descending order.
(b) \(\frac { 1 }{ 5 }\) , \(\frac { 11 }{ 5 }\) , \(\frac { 4 }{ 5 }\) , \(\frac { 3 }{ 5 }\) , \(\frac { 7 }{ 5 }\)
∵ 1, 3, 4, 7 and 11 are in ascending order and 11, 7, 4, 3 and 1 are in descending order.
∴ Fractions in ascending order.
\(\frac { 1 }{ 7 }\) , \(\frac { 3 }{ 7 }\) , \(\frac { 7 }{ 7 }\) , \(\frac { 11 }{ 7 }\) , \(\frac { 13 }{ 7 }\)
Try These (Page 151)
Question 1.
Arrange the following in ascending and descending order:
(a) \(\frac { 1 }{ 12 }\) , \(\frac { 1 }{ 23 }\) , \(\frac { 1 }{ 5 }\) , \(\frac { 1 }{ 7 }\) , \(\frac { 1 }{ 50 }\) , \(\frac { 1 }{ 9 }\) , \(\frac { 1 }{ 17 }\)
(b) \(\frac { 3 }{ 7 }\) , \(\frac { 3 }{ 11 }\) , \(\frac { 3 }{ 5 }\) , \(\frac { 3 }{ 2 }\) , \(\frac { 3 }{ 13 }\) , \(\frac { 3 }{ 4 }\) , \(\frac { 3 }{ 17 }\)
(c) Write 3 more similar examples and arrange them in ascending and descending order.
Solution:
We know that in ‘unlike’ fractions having, same numerator, the greater the value of the denominator, the smaller the value of the fractional number.
(a) ∵ 50, 23, 17, 12, 9, 7 and 5 are in descending order
∴ Fractions in ascending order are:
\(\frac { 1 }{ 50 }\) , \(\frac { 1 }{ 23 }\) , \(\frac { 1 }{ 17 }\) , \(\frac { 1 }{ 12 }\) , \(\frac { 1 }{ 9 }\) , \(\frac { 1 }{ 7 }\) , \(\frac { 1 }{ 5 }\)
(b) ∵ 17, 13, 11, 7, 5, 4 and 2 are in descending order
∴ Ascending order of the given fractions is
\(\frac { 3 }{ 17 }\) , \(\frac { 3 }{ 13 }\) , \(\frac { 3 }{ 11 }\) , \(\frac { 3 }{ 7 }\) , \(\frac { 3 }{ 5 }\) , \(\frac { 3 }{ 4 }\) , \(\frac { 3 }{ 2 }\)
And descending order of the given fractions is
\(\frac { 3 }{ 2 }\) , \(\frac { 3 }{ 4 }\) , \(\frac { 3 }{ 5 }\) , \(\frac { 3 }{ 7 }\) , \(\frac { 3 }{ 11 }\) , \(\frac { 3 }{ 13 }\) , \(\frac { 3 }{ 17 }\)
(c) Three more examples of unlike fractions with the same numerator are:
(i) \(\frac { 2 }{ 13 }\) , \(\frac { 2 }{ 25 }\) , \(\frac { 2 }{ 6 }\) , \(\frac { 2 }{ 8 }\) , \(\frac { 2 }{ 10 }\) , \(\frac { 2 }{ 17 }\)
(ii) \(\frac { 5 }{ 6 }\) , \(\frac { 5 }{ 17 }\) , \(\frac { 5 }{ 14 }\) , \(\frac { 5 }{ 7 }\) , \(\frac { 5 }{ 12 }\) , \(\frac { 5 }{ 8 }\) , \(\frac { 5 }{ 11 }\)
(iii) \(\frac { 4 }{ 11 }\) , \(\frac { 4 }{ 13 }\) , \(\frac { 4 }{ 5 }\) , \(\frac { 4 }{ 7 }\) , \(\frac { 4 }{ 19 }\) , \(\frac { 4 }{ 17 }\) , \(\frac { 4 }{ 15 }\)
Arrange the above in ascending and descending order by yourself
Solution:
(i) Ascending order:
\(\frac { 2 }{ 25 }\) , \(\frac { 2 }{ 17 }\) , \(\frac { 2 }{ 13 }\) , \(\frac { 2 }{ 10 }\) , \(\frac { 2 }{ 8 }\) , \(\frac { 2 }{ 6 }\)
Descending order:
\(\frac { 2 }{ 6 }\) , \(\frac { 2 }{ 8 }\) , \(\frac { 2 }{ 10 }\) , \(\frac { 2 }{ 13 }\) , \(\frac { 2 }{ 17 }\) , \(\frac { 2 }{ 25 }\)
(ii) Ascending order:
\(\frac { 5 }{ 17 }\) , \(\frac { 5 }{ 14 }\) , \(\frac { 5 }{ 12 }\) , \(\frac { 5 }{ 11 }\) , \(\frac { 5 }{ 8 }\) , \(\frac { 5 }{ 7 }\) , \(\frac { 5 }{ 6 }\)
Descending order:
\(\frac { 5 }{ 6 }\) , \(\frac { 5 }{ 7 }\) , \(\frac { 5 }{ 8 }\) , \(\frac { 5 }{ 11 }\) , \(\frac { 5 }{ 12 }\) , \(\frac { 5 }{ 14 }\) , \(\frac { 5 }{ 17 }\)
(iii) Ascending order:
\(\frac { 4 }{ 19 }\) , \(\frac { 4 }{ 17 }\) , \(\frac { 4 }{ 15 }\) , \(\frac { 4 }{ 13 }\) , \(\frac { 4 }{ 11 }\) , \(\frac { 4 }{ 7 }\) , \(\frac { 4 }{ 5 }\)
Descending order:
\(\frac { 4 }{ 5 }\) , \(\frac { 4 }{ 7 }\) , \(\frac { 4 }{ 11 }\) , \(\frac { 4 }{ 13 }\) , \(\frac { 4 }{ 15 }\) , \(\frac { 4 }{ 17 }\) , \(\frac { 4 }{ 19 }\)
Try These (Page 155)
Question 1.
My mother divided an apple into 4 equal parts. She gave me two parts and my brother one part. How many apples did she give to both of us together?
Solution:
On dividing an apple into 4 equal parts, each part of the apple will be 1/4. My mother gave me two parts, i.e., 2/4 parts, and my brother one part, i.e., 1/4 part. The part she gave us together
![]()
Question 2.
Mother asked Neelu and her brother to pick stones from the wheat. Neelu picked one-fourth of the total stones in it and her brother also picked up one-fourth of the stones. What fraction of the stones did both pick up together?
Solution:
Neelu picked one-fourth of the total stones, i.e., 1/4 stones from the wheat and her brother picked up one-fourth of stones, i.e., 1/4 stones. Fractions of stones picked up together by them

![]()
Question 3.
Sohan was putting covers on his notebooks. He put one-fourth of the covers on Monday. He put another one-fourth on Tuesday and the remaining on Wednesday. What fraction of the covers did he put on Wednesday?
Solution:
Sohan put one-fourth of the covers on Monday, i.e., 1/4 covers. He put one-fourth on Tuesday, i.e., 1/4 covers and the remaining on Wednesday. Now, covers put on Monday and Tuesday
![]()
So, covers put on Wednesday

Try These (Page 156)
Question 1.
Add with the help of a diagram.
(i) \(\frac { 1 }{ 8 }\) + \(\frac { 1 }{ 8 }\)
(ii) \(\frac { 2 }{ 5 }\) + \(\frac { 3 }{ 5 }\)
(iii) \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\)
Method I:
Look at the figure. It is divided into 8 equal parts.

Its shaded part = \(\frac { 2 }{ 8 }\)
i.e., \(\frac { 1 }{ 8 }\) + \(\frac { 1 }{ 8 }\) = \(\frac{1+1}{8}\) = \(\frac { 2 }{ 8 }\) or \(\frac { 1 }{ 4 }\)
Method II:
We can also represent the above sum in the following manner:
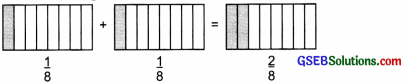
∴ \(\frac { 1 }{ 8 }\) + \(\frac { 1 }{ 8 }\) = \(\frac{1+1}{8}\) = \(\frac { 2 }{ 8 }\)
(ii) \(\frac { 2 }{ 5 }\) + \(\frac { 3 }{ 5 }\)
We have:

Thus, \(\frac { 2 }{ 5 }\) + \(\frac { 3 }{ 5 }\) = \(\frac{2+3}{5}\) = \(\frac { 5 }{ 5 }\) = 1
(iii) \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\)
We have:

Thus, \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\) + \(\frac { 1 }{ 6 }\) = \(\frac{1+1+1}{6}\) = \(\frac { 3 }{ 6 }\) = \(\frac { 1 }{ 2 }\)
Question 2.
add \(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 12 }\) How will we show this pictorially and by using paper folding?
Solution:
\(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 12 }\)
We have:
\(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 12 }\) = \(\frac { 1+1 }{ 12 }\) + \(\frac { 2 }{ 12 }\) = \(\frac { 1 }{ 16 }\)
To show \(\frac { 1 }{ 12 }\) + \(\frac { 1 }{ 12 }\) pictorially, we have:
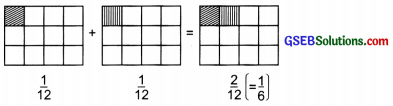
Using paper folding (the activity): Do it yourself.
![]()
Question 3.
Make 5 more examples of problems given in 1 and 2 above. Solve them with your friends.
Solution:
Do it yourself.
Try These (Page 157)
Question 1.
Find the difference between \(\frac { 7 }{ 8 }\) and \(\frac { 3 }{ 8 }\)
Solution:
∵ \(\frac { 7 }{ 8 }\) – \(\frac { 3 }{ 8 }\) = \(\frac { 7-3 }{ 8 }\) and \(\frac { 4 }{ 8 }\) = \(\frac { 1 }{ 2 }\)
∴ The difference between \(\frac { 7 }{ 8 }\) and \(\frac { 3 }{ 8 }\) is \(\frac { 1 }{ 2 }\).
![]()
Question 2.
Mother made a good Patti in a round shape. She divided it into 5 parts. Seema ate one piece from it. If I eat another piece then how much would be left?
Solution:
Total number of equal parts of gud patti = 5
Eaten by Seema = \(\frac { 1 }{ 5 }\)
Eaten by me = \(\frac { 1 }{ 5 }\)
Fraction of gud patti eaten by Seema and me
= \(\frac { 1 }{ 5 }\) + \(\frac { 1 }{ 5 }\) = \(\frac { 1+1 }{ 5 }\) = \(\frac { 2 }{ 5 }\)
∴ Fraction of gud patti left over
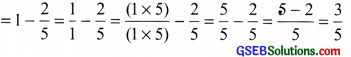
Question 3.
My elder sister divided the watermelon into 16 parts. I ate 7 out of them. My friend ate 4. How much did we eat altogether? How much more of the watermelon did I eat than my friend? What portion of the watermelon remained?
Solution:
Total number of parts =16
The fraction of watermelon eaten
![]()
∴ \(\frac { 3 }{ 16 }\) parts are eaten by us.
Since,[Fraction of watermelon I ate] – [ Fraction of watermelon my friend ate]

∴ I ate \(\frac { 3 }{ 16 }\) portion of watermelon more than my friend.
Now,
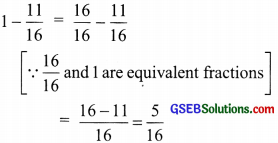
Question 4.
Make five problems of this type and solve them with your friends.
Solution:
Do it yourself.
Try These (page 159)
Question 1.
Add \(\frac { 2 }{ 5 }\) + \(\frac { 3 }{ 7 }\)
Solution:
\(\frac { 2 }{ 5 }\) + \(\frac { 3 }{ 7 }\)
∵ LCM of 5 and 7 = 35

Question 2.
Subtract \(\frac { 2 }{ 5 }\) from \(\frac { 5 }{ 7 }\)
Solution:
\(\frac { 5 }{ 7 }\) – \(\frac { 2 }{ 5 }\)
∵ LCM of 7 and 5 = 35