Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 12 Algebraic Expressions Ex 12.1
![]()
Question 1.
Get the algebraic expressions in the following cases using variables, constants and arithmetic operations.
(i) Subtraction of z from y.
(ii) One-half of the sum of numbers x and y.
(iii) The number z multiplied by itself.
(iv) One-fourth of the product of numbers p and q.
(v) Numbers x and y both squared and added.
(vi) Number 5 added to three times the product of numbers m and n.
(vii) Product of numbers y and z subtracted from 10.
(viii) Sum of numbers a and b subtracted from their product.
Solution:
(i) y – z
(ii) \(\frac { 1 }{ 2 }\)(x + y)
(iii) z²
(iv) \(\frac { 1 }{ 4 }\)pq
(v) x² + y²
(vi) 5 + 3mn
(vii) 10 – yz
(viii) ab – (a + b)
![]()
Question 2.
(i) Identify the terms and their factors in the following expressions. Show the terms and factors by tree diagrams.
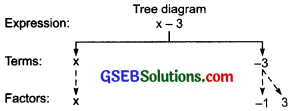
(a) x – 3
(b) 1 + x + x²
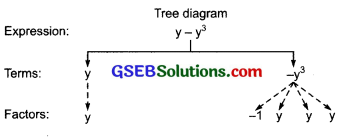
(c) y – y3
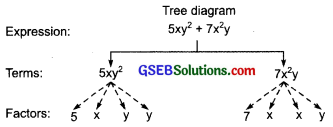
(d) 5xy² + 7x²y
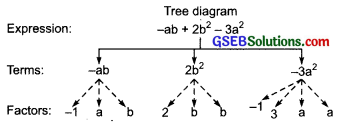
(e) -ab + 2b² – 3a²
(ii) Identify terms and factors in the expressions given below:
(a) -4x + 5
(b) -4x + 5y
(c) 5y + 3y²
(d) xy + 2x²y²
(e) pq + q
(f) 1.2ab – 2.4b + 3.6a
(g) \(\frac { 3 }{ 4 }\)x + \(\frac { 1 }{ 4 }\)
(h) 0.1p² + 0.2q²
Solution:
(i) We have:
(a) x – 3
(b) 1 + x + x²

(c) y – y3
(d) 5xy² + 7x²y
(e) – ab + 2b² – 3a²
(ii)

Question 3.
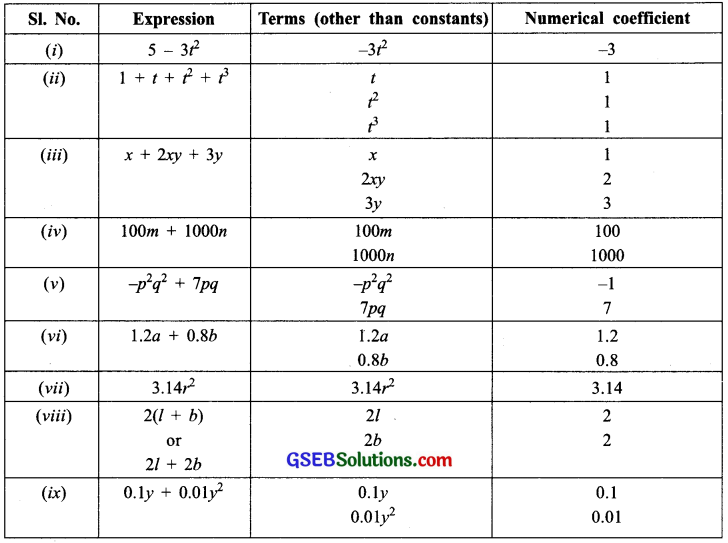
Identify the numerical coefficients of terms (other than constants) in the following expressions:
(i) 5 – 3t²
(ii) 1 + t + t² + t3
(iii) x + 2xy + 3y
(iv) 100m + 1000n
(v) -p²q² + 7pq
(vi) 1.2a + 0.86
(vii) 3.Mr²
(viii) 2(l + b)
(ix) 0.1 y + 0.01 y²
Solution:
Question 4.
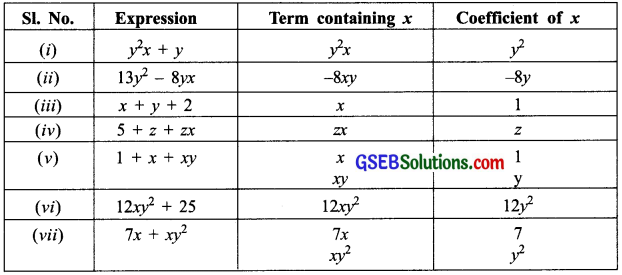
(a) Identify terms which contain x and give the coefficient of x.
(i) yx² + y
(ii) 13y² – 8yx
(iii) x + y + 2
(iv) 5 + z + zx
(v) 1 + x + xy
(vi) 12xy² + 25
(vii) 7x + xy²
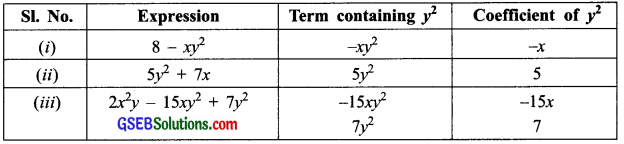
(b) Identify terms which contain y² and give the coefficient of y².
(i) 8 – xy²
(ii) 5y² + 7x
(iii) 2x²y – 15xy² + 7y²
Solution:
(a)
(b)
Question 5.
Classify into monomials, binomials and trinomials.
(i) 4y – 7z
(ii) y²
(iii) x + y – xy
(iv) 100
(v) ab – a – b
(vi) 5 – 3t
(vii) 4p²q – 4pq²
(viii) 7mn
(ix) z² – 3z + 8
(x) a² + b²
(xi) z² + z
(xii) 1 + x + x²
Solution:
(i) 4y – 7z
The expression 4y – 7z is having 2 terms (4y and – 7z).
∴ It is a binomial.
(ii) y²
The expression y² is having only 1 term (y²).
∴ It is a monomial.
(iii) x + y – xy
The expression x + y – xy is having 3 terms (x, y and – xy).
∴ It is a trinomial.
(iv) 100
The expression 100 is having only 1 term (100).
∴ It is a monomial.
(v) ab – a – b
The expression ab – a – b is having 3 terms (ab, – a and – b).
∴ The expression is a trinomial.
(vi) 5 – 3t
The expression 5 – 3t is having two terms (5 and – 3t).
∴ It is a binomial.
(vii) 4p²q – 4pq²
The expression 4p²q – 4pq² is having 2 terms (4p²q and – 4pq²).
∴ It is a binomial.
(viii) 7mn
The expression Imn is having only one term (i.e. Imn).
∴ It is a monomial.
(ix) z² – 3z + 8
The expression z² – 3z + 8 is having 3 terms (i.e. z², – 3z and +8).
∴ It is a trinomial.
(x) a² + b²
The expression (a² + b²) is having 2 terms (i.e. a² and b²).
∴ It is a binomial.
(xi) z² + z
The expression z² + z is having 2 terms (i.e. z² and z).
∴ It is a binomial.
(xii) 1 + x + x²
The expression 1 + x + x² is having 3 terms (i.e. 1, x and x²).
∴ It is a binomial.
![]()
Question 6.
State whether a given pair of terms is of like or unlike terms.
(i) 1, 100
(ii) -7x, \(\frac { 5 }{ 2 }\)x
(iii) -29x, -29y
(iv) 14xy, 42yx
(v) 4m²p, 4mp²
(vi) 12xz, 12x²z²
Solution:
(i) 1, 100 is a pair of like terms (∵ 1 = 1x° and 100 = 100x°)
(ii) -7x, \(\frac { 5 }{ 2 }\) x is a pair of like terms.
(iii) -29x, -29y is a pair of unlike terms.
(iv) 14xy, 42yx is a pair of like terms.
(v) 4m²p, 4mp² is a pair of unlike terms.
(vi) 12xz, 12x²z² is a pair of unlike terms.
![]()
Question 7.
Identify like terms in the following:
(a) – xy², – 4yx², 8x², 2xy², 7y, – 11x², – 100x, – 11yx, 20x²y, – 6x², y, 2xy, 3x
(b) 10qp, 7p, 8q, – p²q², – 7qp, – 100q, – 23, 12q²p², – 5p², 41, 2405p, 78qp, 13q²p, qp², 701p²
Solution:
(a) – xy² and 2xy²; – 4yx² and 20x²y; 8x², 11x² and – 6x²; 7y and y; – 100x and 3x; – 11 yx and 2xy are like terms.
(b) 10qp, – 7qp and 78qp; 7p and 2405p; 8q and – 100q; – p²q² and 12q²p²; – 23 and 41; – 5p² and 701p², 13p²q and qp² are like terms.