Gujarat Board GSEB Textbook Solutions Class 8 Maths Chapter 5 Data Handling Ex 5.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 8 Maths Chapter 5 Data Handling Ex 5.3
Question 1.
List the outcomes you can see in these experiments?
(a) Spinning a wheel

(b) Tossing two coins together
Solution:
(a) Outcomes is spinning the given wheel are: A, B, C or D.
(b) Outcomes in tossing two coins together are: HT, HH, TH, TT
[where HT → Head on first coin + Tail on second coin and so on]
![]()
Question 2.
When a die is thrown, list the outcome of an event of getting
(i) (a) a prime number (b) not a prime number
(ii) (a) a number greater than 5
(b) a number greater than 5.
Solution:
Possible Out comes are: 1, 2, 3, 4, 5 or 6. Out of them prime numbers are 2,3 and 5.
(i) (a) Outcomes of getting a prime number are: 2, 3 or 5.
(b) Outcomes of getting not a prime number are: 1, 4 or 6
(ii) (a) Outcome of getting a number greater than 5 is 6.
(b) Outcomes of getting a number not greater than 5 are: 1, 2, 3, 4 or 5.
Question 3.
Find:
(a) The probability of the pointer stopping on D in
Spinning a wheel

(b) The probability of getting ace from a well shuffled deck of 52 playing cards?
(c) The probability of getting a red apple. (See figure below)
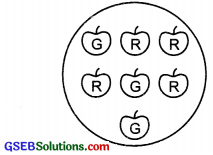
Solution:
(a) On the spinning wheel there are 5 sectors containing A, B, C and D.
Since, there is only 1 sector containing D.
i.e., possible outcome = 1
Number of equally likely outcomes = 5
∴ Probability = \(\frac{1}{5}\)
(b) Number of possible outcomes = 52
Since, there are 4 aces in a pack of 52 cards, and out of them one ace can be obtained in 4 ways.
∴ Equally likely outcomes = 4
∴ Probability of getting an ace = \(\frac{4}{52}\) = \(\frac{1}{13}\)
(c) There are 7 apples in all
∴ Possible number of ways = 7
Since, there are 4 red apples. Therefore, a red apple can be obtained in 4 ways.
i.e., Equally likely outcome = 4
∴ Probability of getting a red apple = \(\frac{4}{7}\)
![]()
Question 4.
Numbers 1 to 10 are written on ten separate slips (one number on one slip), kept in a box and mixed well. One slip is chosen from the box without looking into it. What is the probability of:
- getting a number 6?
- getting a number less than 6?
- getting a number greater than 6?
- getting a 1 – digit number?
Solution:
Since, there are 10 slips. At a time any slip can be taken out.
∴ Number of total outcomes = 10
Now,
1. We can get a slip containing the number ‘6’ only once.
∴ Number of favourable outcome = 1
Thus, probability of getting the number 6 = \(\frac{1}{10}\)
2. There are five numbers (i.e., 1, 2, 3, 4 and 5) which are less than 6.
Favourable outcomes are 5.
∴ Thus, probability of getting a number less than six = \(\frac{5}{10}\) = \(\frac{1}{2}\)
3. There are 4 numbers (i.e., 7, 8, 9, 10) which are greater than six.
∴ Favouable outcomes = 4
Thus, probability of getting a number greater than six = \(\frac{4}{10}\) = \(\frac{2}{5}\)
4. There are nine one-digit numbers
i.e., (1, 2, 3, 4, 5, 6, 7, 8 and 9)
∴ Favourable outcomes = 9
Thus, probability of getting a one-digit number = \(\frac{9}{10}\)
![]()
Question 5.
If you have a spinning wheel with 3 green sectors, 1 blue sector and 1 red sector, what is the probability of getting a green sector? What is the probability of getting a non-blue sector?
Solution:
There are 5 sectors in all (3 green + 1 blue + 1 red).
∴ There are total possible outcomes = 5.
Since, there are 3 green sectors.
i.e., Number of favourable outcomes = \(\frac{3}{5}\)
Thus, probability of getting a green sector = \(\frac{3}{5}\)
Again, there are 4 non-blue sectors.
∴ Favouable outcomes = 4
Thus, probability of getting a ‘non-blue’ sector = \(\frac{4}{5}\)
![]()
Question 6.
Find the probabilities of the events given in Question 2?
Solution:
There are 6 outcomes in all (i.e., 1, 2, 3, 4, 5, 6)
1. Since, there are 3 prime numbers (i.e., 2, 3, and 5)
∴ Favourable outcomes = 3
Thus, probability of getting a prime number = \(\frac{3}{6}\) = \(\frac{1}{2}\)
2. Since, there are 3 non-prime numbers (i.e., 1, 4 and 6)
∴ Favourable outcomes = 1
Thus, the probability of getting a non-prime number = \(\frac{3}{6}\) = \(\frac{1}{2}\)
3. Since, there is 1 number greater than 5 (i.e, 6)
∴ Favourable outcome = 1
Thus, probability of a number greater than 5 = \(\frac{1}{6}\)
4. Since, there are 5 numbers which are not greater than 5 (i.e, 1, 2, 3, 4 and 5)
∴ Number of favourable outcomes = 5 Thus, the probability of a number which is not greater than 5 = \(\frac{5}{6}\)