Gujarat Board GSEB Textbook Solutions Class 7 Maths Chapter 8 Comparing Quantities Ex 8.3 Textbook Questions and Answers.
Gujarat Board Textbook Solutions Class 7 Maths Chapter 8 Comparing Quantities Ex 8.3
![]()
Question 1.
Tell what is the profit or loss in the following transactions. Also find profit per cent or loss per cent in each case.
(a) Gardening shears bought for ₹ 250 and sold for ₹ 325.
(b) A refrigerate bought for ₹ 12,000 and sold at ₹ 13,500.
(c) A cupboard bought for ₹ 2,500 and sold at ₹ 3,000.
(d) A skirt bought for ₹ 250 and sold at ₹ 150.
Solution:
(a) Cost price (CP) = ₹ 250
Selling price (SP) = ₹ 325
∵ CP < SP so there is a profit.
∴ Profit = SP – CP
= ₹ 325 – ₹ 250 = ₹ 75
Now, Profit % = \(\frac { Profit }{ CP }\) x 100%
= \(\frac { 75 }{ 250 }\) x 100 % = 30%
(b) Cost price (CP) = ₹ 12,000
Selling price (SP) = ₹ 13,500
∵ CP < SP, so there is a profit.
∴ Profit = SP – CP = ₹ 13,500 – ₹ 12,000 = ₹ 1,500
Now, Profit % = \(\frac { Profit }{ CP }\) x 100%
= \(\frac { 1500 }{ 12000 }\) x 100%
= \(\frac { 150 }{ 12 }\)
= 12.5%
(c) Cost price (CP) = ₹ 2500
Selling price (SP) = ₹ 3000
∵ CP < SP, so there is a profit.
∴ Profit = SP – CP = ₹ 3000 – ₹ 2500 = ₹ 500
Now, Profit % = \(\frac { Profit }{ CP }\) x 100%
= \(\frac { 500 }{ 2500 }\) x 100% = 20%
(d) Cost price (CP) = ₹ 250
Selling price (SP) = ₹ 150
∵ CP > SP,
so there is a loss.
∴ Loss = CP – SP
= ₹ 250 – ₹ 150 = ₹ 100
Now, Loss % = \(\frac { Profit }{ CP }\) x 100%
= \(\frac { 100 }{ 250 }\) x 100% = 40%
Question 2.
Convert each part of the ratio to percentage:
(a) 3 : 1
(b) 2 : 3 : 5
(c) 1 : 4
(d) 1 : 2 : 5
Solution:
(a) 3:1
Total of the parts = 3 + 1 = 4
∴ Percentage of the 1st part of the ratio
= \(\frac { 3 }{ 4 }\) x 100% = 75%
Percentage of the 2nd part of the ratio = \(\frac { 1 }{ 4 }\) x 100% = 25%
(b) 2 : 3 : 5
Total of the parts = 2 + 3 + 5 = 10
∴ Percentage of 1st part of the ratio
= \(\frac { 2 }{ 10 }\) x 100% = (2 x 10)% = 20%
Percentage of 2nd part of the ratio
= \(\frac { 3 }{ 10 }\) x 100% = (3 x 10)% = 30%
Percentage of 3rd part of the ratio
= \(\frac { 5 }{ 10 }\) x 100% = (5 x 10)% = 50%
(c) 1 : 4
Total of parts = 1 + 4 = 5
∴ Percentage of the 1st part of the ratio
= \(\frac { 1 }{ 5 }\) x 100% = (1 x 20)% = 20%
Percentage of the 2nd part of the ratio
= \(\frac { 4 }{ 5 }\) x 100% = (4 x 20)% = 80%
(d) 1 : 2 : 5
Total of the parts = 1 + 2 + 5 = 8
∴ Percentage of the 1st part of the ratio
= \(\frac { 1 }{ 8 }\) x 100% = \(\frac { 25 }{ 2 }\) = 12.5%
Percentage of the 2nd part of the ratio
= \(\frac { 2 }{ 8 }\) x 100% = 25%
Percentage of the 3rd part of the ratio
= \(\frac { 5 }{ 8 }\) x 100% = \(\frac { 125 }{ 2 }\) % = 62.5%
![]()
Question 3.
The population of a city decreased from 25,000 to 24,500. Find the percentage decrease.
Solution:
Initial population = 25,000
Decreased population = 24,500
Decrease in population = 25,000 – 24,500 = 500

Question 4.
Arun bought a car for ₹ 3,50,000. The next year, the price went upto ₹ 3,70,000. What was the percentage, of price increase?
Solution:
Initial cost = ₹ 3,50,000
Increased cost = ₹ 3,70,000
Increase in cost
= ₹ 3,70,000 – ₹ 3,50,000
= ₹ 20,000
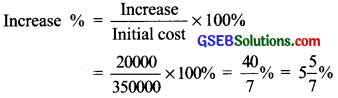
Question 5.
1 buy a T.V for ₹ 10,000 and sell it at a profit of 20%. How much money do I get for it?
Solution:
CP of the T.V. = ₹ 10,000
Profit percent = 20%
∴ Profit = 20% of 10,000
= ₹ \(\frac { 20 }{ 100 }\) x 10,000
= ₹ 2,000
Now, SP = CP + Profit
Thus, I will get ₹ 12,000 for the T.V.
= ₹ 10,000 + ₹ 2,000 = ₹ 12,000
Thus, I will get ₹ 12,000 for the T.V.
Question 6.
Juki sells a washing machine for ₹ 13,500. She loses 20% in the bargain. What was the price at which she bought it?
Solution:
Selling price (SP) = ₹ 13,500
Loss % = 20%
CP = ?
∴ CP – Loss = SP
∴ CP – (20% of CP) = ₹ 13,500
= ₹ 13,500
or CP – \(\frac { 20 }{ 100 }\)CP = ₹ 13,500
or \(\frac { 5CP – CP }{ 5 }\) = ₹ 13,500
or \(\frac { 4 }{ 5 }\)CP = ₹ 13,500
⇒ CP = ₹ 13,500 x \(\frac { 5 }{ 4 }\)
= ₹ 3,375 x 5
= ₹ 16,875
∴ Juhi bought the washing machine for ₹ 16,875.
![]()
Question 7.
(i) Chalk contains calcium, carbon and oxygen in the ratio 10 : 3 : 12. Find the percentage of carbon in chalk.
(ii) If in a stick of chalk, carbon is 3 g, what is the weight of the chalk stick?
Solution:
(i) ∵ The ratio of calcium, carbon and oxygen in mixture is 10 : 3 : 12.
∴ Total of ratios = 10 + 3 + 12 = 25
∴ Percentage of carbon in the chalk mixture
= \(\frac { 3 }{ 25 }\)
(ii) Let the weight of the stick be x g.
∵ 12% of the chalk mixture is 3 g.
∴ 12% of x = 3
or \(\frac { 12 }{ 100 }\) × x = 3 ⇒ x = \(\frac { 3×100 }{ 12 }\) = 25
or Weight of the chalk stick = 25 g.
Question 8.
Amina buys a book for ₹ 215 and sells it at a loss of 15%. How much does she sell it for?
Solution:
Cost price of the book (CP) = ₹ 275
Loss % = 15%
∴ Loss = 15% of CP = ₹ \(\frac { 15 }{ 100 }\) x 275
= ₹ \(\frac { 15×11 }{ 4 }\)
= ₹ \(\frac { 165 }{ 4 }\)
= ₹ 41.25
Now SP = CP – Loss
= ₹ 275 – ₹ 41.25
= ₹ 233.75
Thus, Amina will sell the book for ₹ 233.75.
Question 9.
Find the amount to be paid at the end of 3 years in each case:
(a) Principal = ₹ 1,200 at 12% p.a.
(b) Principal = ₹ 7,500 at 5% p.a.
Solution:
(a) Here, Principal (P) = ₹ 1,200
Rate (R) = 12% p.a. and Time (T) = 3 years
∴ Interest = \(\frac { P×R×T }{ 100 }\) = ₹\(\frac { 1,200×12×3 }{ 100 }\)
₹ (12 x 12 x 3) = ₹ 432
Now, Amount = Principal + Interest
= ₹ 1,200 + ₹ 432 = ₹ 1,632
(b) Principal (P) = ₹ 7,500
Rate (R) = 5% p.a.
Time (T) = 3 years
∴ Interest = \(\frac { P×R×T }{ 100 }\) = ₹\(\frac { 7,500×5×3 }{ 100 }\)
= ₹ (75 x 5 x 3) = ₹ 1,125
Now, Amount = Principal + Interest
= ₹ 7,500 + ₹ 1,125 = ₹ 8,625
![]()
Question 10.
What rate gives ₹ 280 as interest on a sum of ₹ 56,000 in 2 year?
Solution:
Principal (P) = ₹ 56,000
Rate (R) = ?
Time (T) = 2 years
Interest = ₹ 280
∵ Interest = \(\frac { P×R×T }{ 100 }\)
∴ 280 = \(\frac { 56,000×R×2 }{ 100 }\)
or R = \(\frac { 280×100 }{ 2×56,000 }\) = \(\frac { 1 }{ 4 }\)% = 0.25%
Thus, 0.25% p.a. of interest rate will give the required interest.
Question 11.
If Meena gives an interest of ₹ 45 for one year at 9% rate p.a. What is the sum she has borrowed.
Solution:
rincipal (P) = ?
Rate (R) = 9% p.a.
Interest = ₹ 45
Time (T) = 1 year
Since Interest = \(\frac { P×R×T }{ 100 }\)
or ₹ 45 = \(\frac { 45×100 }{ 9 }\)
= ₹ 5 x 100
= ₹ 500